Este es uno de los métodos más antiguos para encontrar una raíz real de una ecuación f(x)=0 y se asemeja bastante al método de bisección.
En este método se seleccionan dos puntos x0 y x1 de forma que f(x0) y f(x1) son de signos contrarios. Es decir, el grafico de la función y=f(x) cruza el eje x entre estos dos puntos.
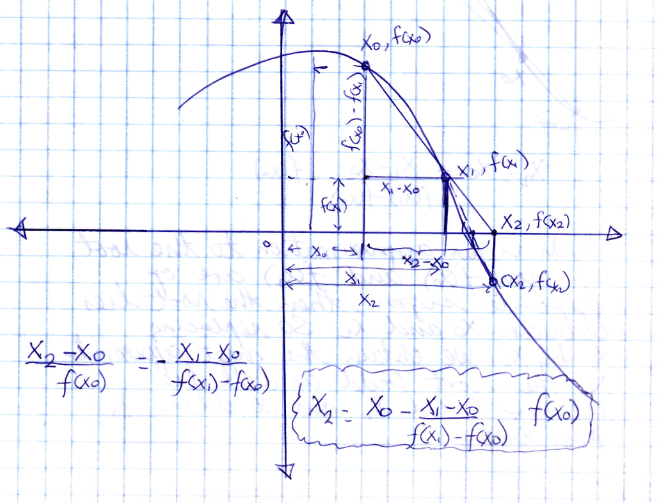
Aunque si ambos valores de la función en los puntos x0 y x1 no son de signo contrario es posible que el método converja a una solución si la raíz se encuentra en las cercanías de esos puntos.
El valor encontrado de x2 no es una raíz, sino una aproximación, que se encuentra en la intersección con el eje X de la recta que pasa por los puntos (x0 , f(x0)) y (x1 , f(x1)). Si ahora los valores de f(x0) y f(x2) son de signos opuestos, entonces la raíz cae entre los puntos x0 y x2, así que reemplazando x1 por x2 obtendremos la siguiente aproximación. El proceso se repite hasta que el valor de la aproximación se acerque a cero de acuerdo a un nivel de tolerancia establecida.
Encontrar la raíz real de la ecuación
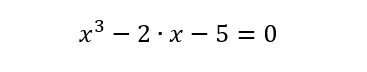
Utilizando el método de la falsa posición (Regula falsi)
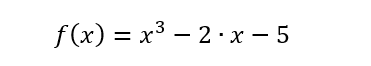
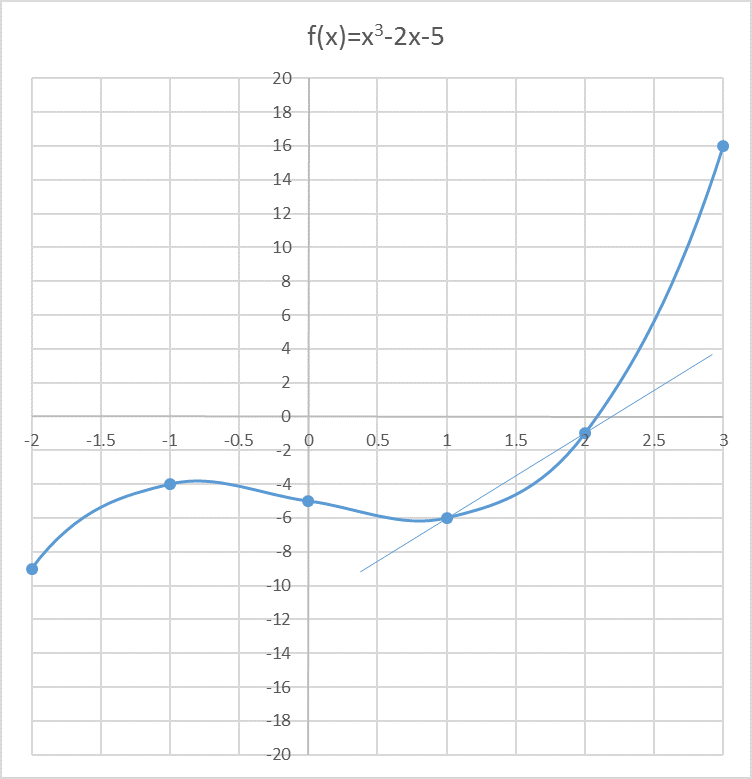
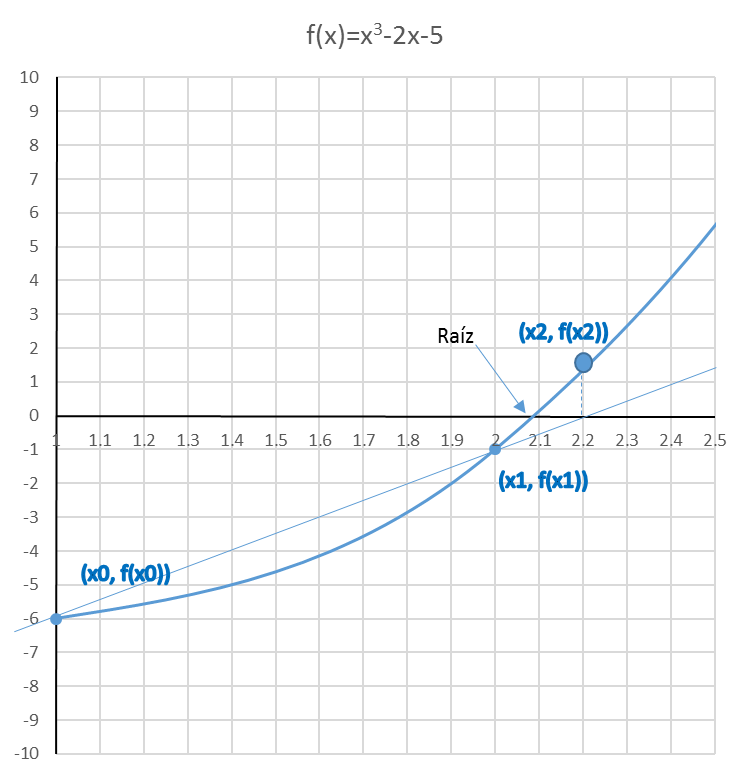
Primera Aproximación (iteración 1)
Comenzamos evaluando la función en los valores x0=1 y x1=2
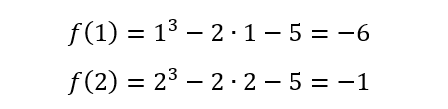
Ambos valores de f(x) son negativos.
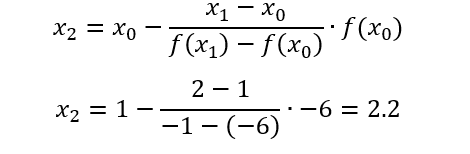
La primera aproximación x2=2.2
Ahora calculamos que punto que está más cerca de la aproximación que hemos calculado.
Para eso comparamos los valores absolutos de la diferencia de cada punto con respecto a x2.
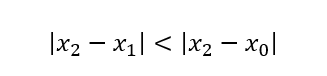
Si esta condición se cumple entonces hacemos:
x0=x1 y x1=x2
Es decir, si el valor de x1 está más de cerca de x2, entonces x0 toma el valor de x1 y x1 adopta el valor de x2 y se realiza una nueva iteración.
Segunda iteración
0.2<1.2
Entonces
x0=x1 y x1=x2
x0=2 y x1=2.2
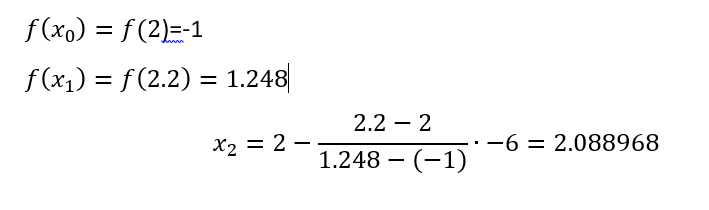
x2-x1=0.111032
x2-x0=0.08896
Como el valor absoluto de x2 – x1 no es menor que el valor absoluto de x2-x0
Entonces
Tercera Iteración
x0=x0 y x1=x2
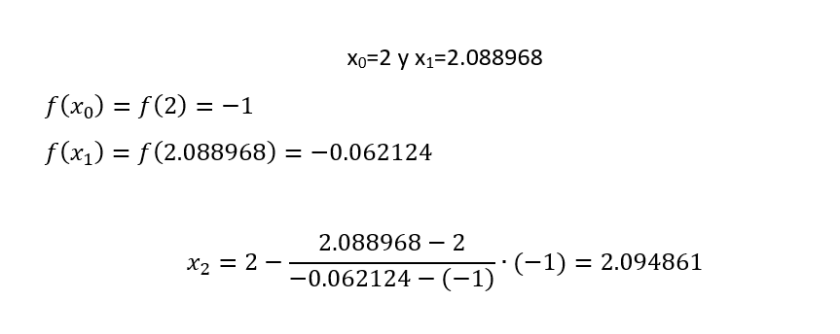
Como el valor absoluto de x2 – x1 es menor que el valor absoluto de x2-x0
Entonces
Cuarta Iteración
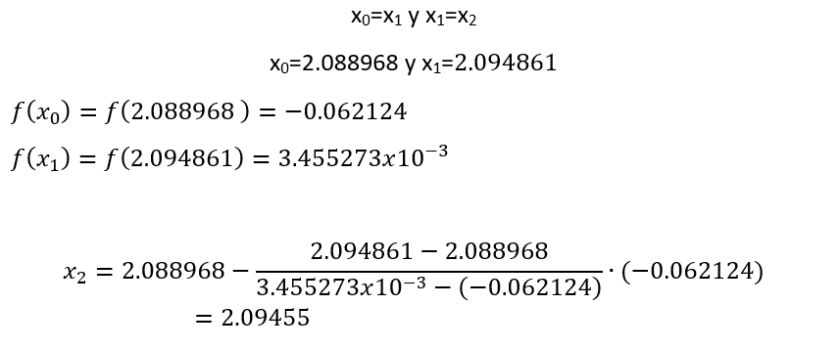
Como el valor absoluto de x2 – x1 es menor que el valor absoluto de x2-x0
Entonces
Quinta Iteración

En resumen, tenemos que a través de sucesivas iteraciones nos acercamos más al valor de la raíz de f(x). Podemos continuar hasta alcanzar la diferencia requerida.
| Iteración | x0 | x1 | x2 | F(x2) |
| 1 | 1 | 2 | 2.2 | 1.2480 |
| 2 | 2 | 2.2 | 2.088968 | -0.06212 |
| 3 | 2 | 2.088968 | 2.094861 | 0.00345 |
| 4 | 2.088968 | 2.094861 | 2.094550 | -1.088E-05 |
| 5 | 2.094861 | 2.094550 | 2.094551 | -1.898E-09 |
Un seudocódigo para un algoritmo que implementa el método de regula falsi se muestra a continuación
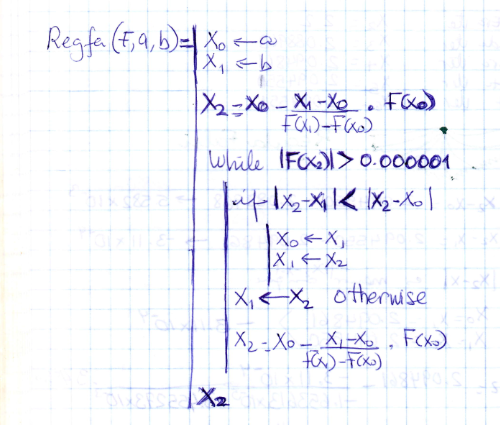
Mientras que el valor de f(x2) sea mayor a la tolerancia establecida continuara en el ciclo iterativo. Una vez que se alcanza la tolerancia establecida el valor de x2 representa la mejor aproximación a la raíz.
